RefleCube: a reflection on the Rubik's Cube

Solvers of the Rubik's Cube are used to the parity constraints, for example, the impossibility of twisting one corner by itself. But the mirror moves here allow us to do more.

Gallery of wacky phenomena

On "Mirror +":

You may swap a pair of edge pieces, for example, yellow/blue <=> yellow/green: (front/back view)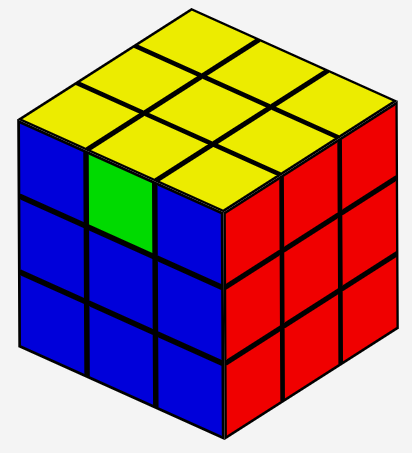

On "Mirror X":

You may swap a pair of corner pieces, for example, yellow/blue/red <=> yellow/green/orange: (front/back view)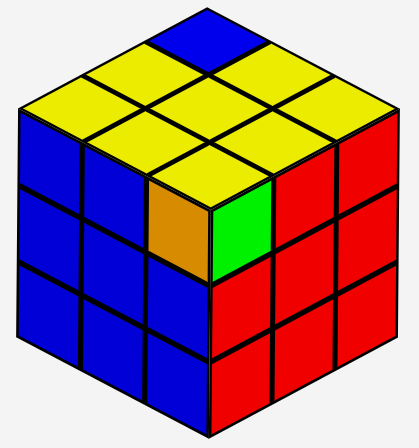

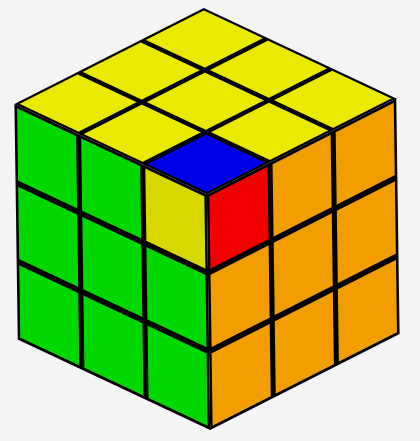
or mirror a pair of corner pieces, for example, yellow/blue/red <=> yellow/green/orange: (front/back view)

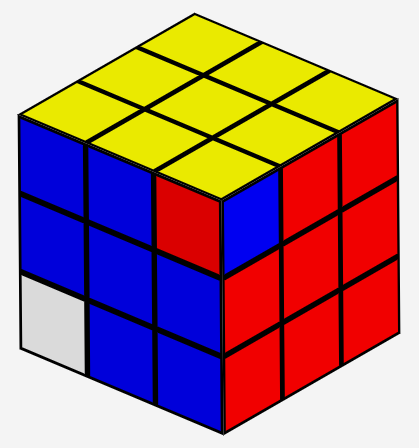
or even twist a corner by itself, for example, yellow/blue/red:

On "Mirror & twist":

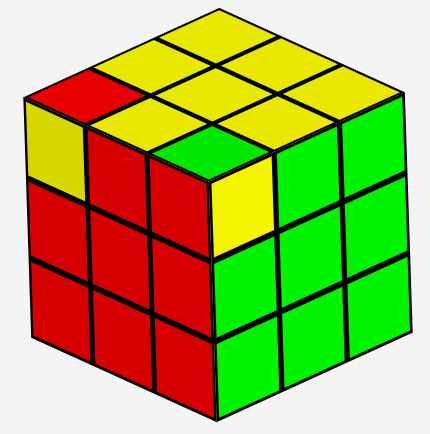
You may, naturally, do all of the above things. In addition, you may mirror swap a pair of adjacent corners, which is not even possible on "Mirror X": (front/back view)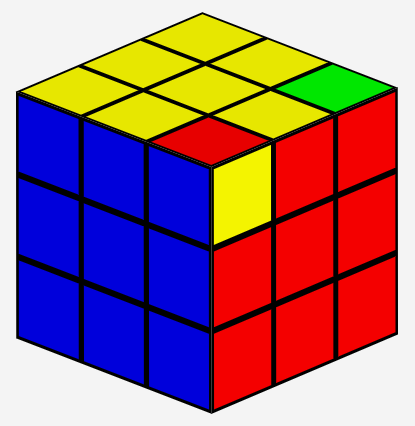

On "4x4x4: Mirror X":

You may mirror a pair of edge pieces in place, or swap a pair of them.

Number of permutations

I understand the number of permutations (states) of a puzzle has almost nothing to do with its difficulty. But just in case you are curious, here are the number of permutations of the 3x3x3 puzzles.

Half turn cube:	663552	Subgroup of all the other puzzles here
Mirror +:	18579456
Rubik's Cube:	43252003274489856000
Mirror X:	118634066124315033600	(96/35=2.74 times that of the Rubik's cube)
Mirror & twist:	33217538514808209408000	768 times that of the Rubik's cube

The half turn cube is a subgroup of everything else, because mirroring across perpendicular directions turns a layer by 180 degrees. The group of Mirror X is even larger than that of the Rubik's Cube.

Here is the GAP code I used to compute these numbers. They provide insights when exploring the possible transforms.

Back to the puzzle